Triángulos rectángulos: ¿Qué elementos tienen? ¿Cómo se relacionan los elementos de un triángulo rectángulo?
Los triángulos en general, están formados por 3 lados y 3 ángulos. Además, los triángulos rectángulos se llaman así por tener un ángulo recto entre sus catetos.
Los lados de un triángulo rectángulo son la hipotenusa y los dos catetos:
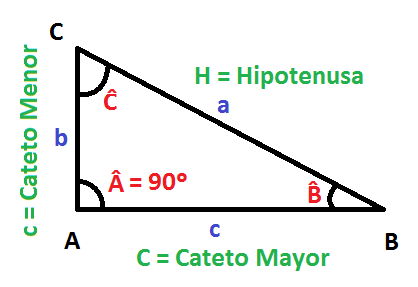
El lado que está enfrente del ángulo recto es la hipotenusa:
![]()
A los otros dos lados, son los catetos: cateto mayor y cateto menor, que como su propio nombre indican, el cateto mayor es el que tiene una mayor longitud y el cateto menor es el que tiene una menor longitud.
Pero existe otra forma de denominar a los catetos, en función del ángulo que tomemos de referencia: el cateto opuesto y contiguo (o cateto adyacente).
¿Cómo identificar los catetos en un triángulo rectángulo?
Te voy a explicar cómo diferenciar entre el cateto opuesto y el cateto contiguo en función del ángulo de referencia.
¿Cómo saber cuál es el cateto opuesto?
Se le llama cateto opuesto al lado que esté enfrente del ángulo de referencia
¿Cómo saber cuál es el cateto contiguo o cateto adyacente?
Se le llama cateto contiguo al lado que esté tocando a ese ángulo.
Por ejemplo, en este triángulo:

Si tomamos de referencia el ángulo B:

b es el lado que está enfrente de B y c es el lado que está tocando al ángulo B.
Pero si tomamos como referencia al ángulo C:

Entonces b es el cateto contiguo y c es el cateto opuesto.
Por tanto, para saber cuál de todas las razones trigonométricas en el triángulo rectángulo, tienes que utilizar para resolver un problema, lo primero que tienes que hacer es identificar tus catetos con respecto al ángulo con el que estés calculándolas.
Los lados y ángulos del triángulo rectángulo, tienen una serie de relaciones entre ellos, las cuales nos van a ayudar a calcular las medidas de los elementos que no conozcamos.
- Los tres lados están relacionados por el teorema de Pitágoras:
![]()
- Los tres ángulos suman entre ellos 180º:
![]()
- Los lados y los ángulos se relacionan mediante las razones trigonométricas, las cuales te las explico con todo detalle en el siguiente apartado.
Razones trigonométricas de un triángulo rectángulo
Los ángulos y lados de un triángulo rectángulo, están relacionados por unas expresiones a las que llamamos razones trigonométricas.
Vamos ir viéndolas una por una, tomando como ángulo de referencia el ángulo B.
Seno del ángulo B
Relaciona el ángulo B con el cateto opuesto y la hipotenusa. En otras palabras, es la razón entre el cateto opuesto y la hipotenusa. Se expresa como sen B:
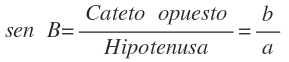
Coseno del ángulo B
Relaciona el ángulo B con el cateto contiguo y la hipotenusa. Es la razón entre el cateto contiguo y la hipotenusa. Se expresa como cos B:
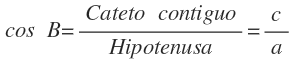
Tangente del ángulo B
Es la razón entre el cateto opuesto y el cateto contiguo. También entre el seno y el coseno. Se expresa como tg B:

Cosecante del ángulo B
Es la razón inversa del seno. Se expresa como cosec B:

No hay que confundirlo con la función inversa del seno, que es el arco seno.
Secante del ángulo B
Es la razón inversa del coseno. Se expresa como sec B:

No hay que confundirlo con la función inversa del coseno que es el arco coseno.
Cotangente del ángulo B
Es la razón inversa de la tangente y se expresa como cotg B:
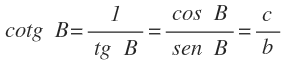
No hay que confundirlo por la función inversa de la tangente que es el arco tangente.
Como ves, todas la razones trigonométricas relacionan un ángulo con dos lados, es decir, tres variables. Por tanto, a la hora de elegir que razón utilizar, deberá ser aquella que sepamos al menos dos de las tres variables.
Tenemos que ir jugando con estas fórmulas según los datos que nos de el enunciado del problema.
Existen dos casos posibles que podemos encontrarnos en los problemas o ejercicios de resolución de triángulos rectángulos que son:
- Que conozcamos dos lados y nos pregunte por algún ángulo o el otro lado
- Que conozcamos un lado y un ángulo y nos pidan calcular cualquier otro lado o ángulo
Si nos dan como dato dos ángulos, no podremos calcular los lados de ese triángulo rectángulo. Necesitaríamos más información.
Siempre necesitamos como mínimo dos datos para calcular un tercero.
Resolución de triángulos rectángulos cuando se conocen dos lados
Vamos a ver, todo lo que te acabo de explicar con un ejemplo. Tenemos un triángulo del que conocemos 2 de sus lados:
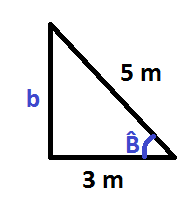
Nos piden calcular el lado b y el ángulo B:
Para calcular el lado b, lo hacemos mediante la fórmula de Pitágoras, ya que en esa fórmula se relacionan los 3 lados y sólo nos queda por conocer 1 un lado.
De la fórmula de Pitágoras despejamos el cateto mayor, que corresponde con el lado b:

Y ahora sustituimos valores y calculamos:
- C = b (es el lado que estamos calculando)
- c = 3 m
- H = 5 m

Nos ha quedado una ecuación, de la que tenemos b como incógnita.
Para calcular el ángulo B, podemos hacerlo de muchas maneras. Una de ellas es utilizando la razón trigonométrica del seno por ejemplo, ya que conocemos el valor de la hipotenusa y del cateto opuesto.
En realidad podríamos utilizar cualquier razón trigonométrica porque conocemos todos sus lados:

Sustituimos valores y resolvemos:

Una vez conocemos el valor del seno de B, con la calculadora hemos calculado su inversa y obtenemos el ángulo. Presta atención a que la calculadora esté en grados y no en radianes.



