Matecho Vicentinas

Radianes

Un radián es la unidad de medida de un ángulo con vértice en el centro de un círculo cuyos lados son cortados por el arco de la circunferencia, y que además dicho arco tiene una longitud igual a la del radio.

El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios dividida entre el radio; es decir, θ = s/r, donde θ es el ángulo, s es la longitud de arco, y r es el radio. Por tanto, el ángulo completo, {\displaystyle \scriptstyle {\theta }_{\text{circunferencia}}} que subtiende una circunferencia de radio r, medido en radianes, es:

{\displaystyle \theta _{\text{circunferencia}}={\frac {L_{\text{circunferencia}}}{r}}={\frac {2\pi r}{r}}=2\pi \ {\text{rad}}\,}

El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.

El radián es la unidad natural en la medida de los ángulos. Por ejemplo, la función seno de un ángulo x expresado en radianes cumple:

${\displaystyle \lim _{x\rightarrow 0}{\frac {\operatorname {sen}(x)}{x}}=1}$

Análogamente los desarrollos Taylor de las funciones seno y coseno son:

• ${\displaystyle \operatorname {sen}(x)=x-{\frac {x^{3}}{3!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}}$

• ${\displaystyle \cos(x)=1-{\frac {x^{2}}{2!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}}$

La tabla muestra la conversión de los ángulos más comunes.

El radián tiene una unidad derivada llamada radián por segundo (rad/s), que corresponde a la magnitud velocidad angular. Esta unidad tiene una equivalencia con las rpm. Las equivalencias se pueden calcular fácilmente haciendo la siguiente relación:Otras unidades de medida de ángulos convencionales son el grado sexagesimal, el grado centesimal y, en astronomía, la hora.

${\displaystyle {\rm {rpm={\frac {rev}{min}}={\frac {2\pi \ rad}{60\ s}}}}}$, que simplificada es: ${\displaystyle {\rm {rpm={\frac {\pi }{30}}{\frac {rad}{s}}}}}$, o bien: ${\displaystyle {\rm {{\frac {rad}{s}}={\frac {30}{\pi }}\ rpm}}}$.

Es decir que, para pasar una cantidad x de rpm a rad/s tenemos que multiplicarla por π/30:

${\displaystyle x{\rm {\ rpm\cdot {\frac {{\frac {\pi }{30}}\ rad/s}{rpm}}=}}}$${\displaystyle \;x\cdot {\frac {\pi }{30}}{\rm {\ rad/s=}}}$${\displaystyle \;x'{\rm {\ rad/s}}}$

Análogamente, para pasar una cantidad y de rad/s a rpm tenemos que multiplicarla por 30/π:

${\displaystyle y{\rm {\ rad/s\cdot {\frac {{\frac {30}{\pi }}\ rpm}{rad/s}}=}}}$${\displaystyle \;y\cdot {\frac {30}{\pi }}{\rm {\ rpm=}}}$${\displaystyle \;y'{\rm {\ rpm}}}$

Grados sexagesimales y radianes. 

Para medir los ángulos se pueden utilizar dos unidades: los grados sexagesimales y los radianes. Ambas unidades son equivalentes

¿Y qué significa que sean equivalentes?

Pues que para el mismo ángulo, su valor lo puedes dar en ángulos o en radianes y por tanto se puede convertir de una unidad a otra.

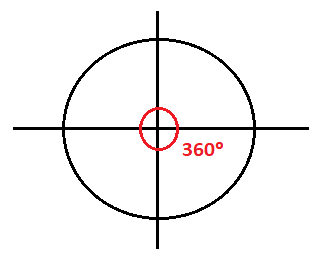
Normalmente, estamos más familiarizados con los grados, ya que es lo primer que nos enseñan. Como ya sabes, una vuelta completa de circunferencia tiene 360º:

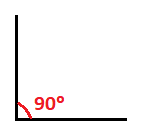
Un ángulo recto mide 90º :

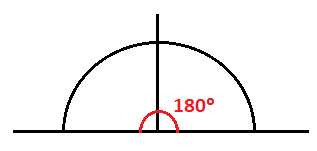
O una semicircunferencia tiene 180º:

Esos mismos ángulos también se pueden medir en radianes.

Una circunferencia tiene 2π radianes:

Un ángulo recto tiene π/2 radianes:

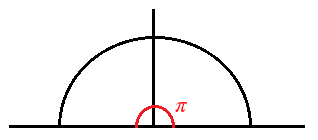
Y una semicircunferencia mide π radianes:

Los radianes se escriben como múltiplos de π, siempre que sea posible, aunque no es obligatorio, pero es más cómodo trabajar con mútliplos de π, que ir arrastrando decimales. Además es mucho más exacto.

Pero, ¿cuál es la equivalencia entre grados y radianes?

Equivalente entre grados y radianes

La equivalencia entre grados y radianes es la siguiente:

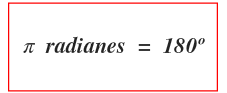
Cómo pasar de grados a radianes paso a paso

Para pasar de grados a radianes lo hacemos mediante una regla de tres, teniendo en cuenta la equivalencia entre radianes y grados.

Por ejemplo, ¿cuántos radianes son 60º?

Planteamos la regla de tres: Si 180º son π radianes, 60º serán x radianes. Ponemos los grados debajo de los grados y los radianes debajo de los radianes:

Y ahora despejamos la x:

Ya sólo nos queda operar. Para dejarlo el resultado en múltiplos de π , simplificamos los números que tenemos en la operación y nos queda:

Por tanto, 60º equivalen a π /3 radianes:

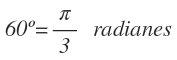
Como te he comentado antes, no es obligatorio dejar los radianes en función de π , por lo que si te es más fácil, puedes sustituir π  por 3,14 y operar con la calculadora, cuyo resultado será:

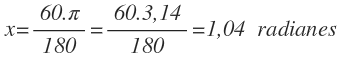
Cómo pasar de radianes a grados paso a paso

Para pasar de radianes a grados, lo hacemos igual que antes, con una regla de 3, solo que esta vez, la incógnita a despejar serán los grados.

Vamos a verlo con un ejemplo:

¿Cuántos grados son 3π /4 radianes?

Planteamos la regla de tres: Si π radianes son 180º, 3π/4 radianes seran x grados:

Despejamos la x y resolvemos:

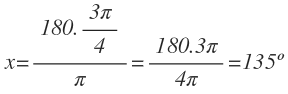
Por tanto 3π/4 radianes equivalen a 135º

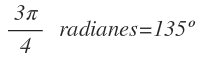
Grados y radianes en las razones trigonométricas con la calculadora

Para calcular las razones trigonométricas tanto en grados como en radianes es necesario que la calculadora la pongas en modo «grados» o en modo «radianes».

Por defecto, la calculadora está en «grados» y para trabajar con radianes hay que cambiarla a «radianes», pero mucho cuidaddo, porque es muy habitual cambiarla a «radianes» y olvidarse y luego trabajar con grados, entonce estará todo mal.

Asegúrate que la calculadora está siempre en el modo que quieres.

Si calculas el seno de 90º con la calculadora (que por defecto está en «grados»), verás que el resultado es 1:

Si pasas 90º a radianes, verás que 90º=π/2 radianes, por lo que el seno de π/2 también es 1:

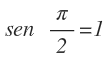
Sin embargo, si calculas el seno de π/2 con la calculadora en «grados», el resultado no será el correcto, ya que te dará 0,027:

Ya que realmente estarás calculando el seno de 1,57º (que es el resultado de dividir π entre 2).

Para calcular el seno de π/2  correctamente y que el resultado sea 1, entonces la calculadora debe estar en «radianes».

Es un despiste muy frecuente, así que asegúrate siempre de que la tienes en el modo correcto.