Introducción
La notación científica nos permite escribir números muy grandes o muy pequeños de forma abreviada. Esta notación consiste simplemente en multiplicar por una potencia de base 10 con exponente positivo o negativo.
Ejemplo: el número 0,00000123 puede escribirse en notación científica como
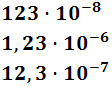Evitamos escribir los ceros decimales del número, lo que facilita tanto la lectura como la escritura del mismo, reduciendo la probabilidad de cometer erratas.
Obsérvese que existen múltiples posibilidades de expresar el mismo número, todas ellas igualmente válidas.
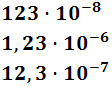
Obsérvese que existen múltiples posibilidades de expresar el mismo número, todas ellas igualmente válidas.
En esta página veremos cómo escribir números naturales y decimales en notación científica y viceversa. Las operaciones (multiplicar, dividir, sumar y restar) entre números escritos de este modo las veremos en otra página.
1. Potencias de 10
Recordatorio del significado y valor de las potencias de base 10 con exponente positivo y con exponente negativo.2. Multiplicar/dividir por 10
La notación científica consiste precisamente en multiplicar por una potencia de 10. En esta sección explicamos el resultado de multiplicar o dividir un número por 10 para comprender el resultado de multiplicar por una potencia de 10.3. Multiplicar por una potencia de 10 con exponente Positivo
En el apartado anterior vimos que al multiplicar un número por 10 la coma decimal de dicho número se desplaza una posición hacia la derecha.
Como multiplicar sucesivamente (varias veces) por 10 es lo mismo que multiplicar por una potencia de 10,
Al multiplicar un número por la potencia 10n (con exponente positivo) se desplaza la coma hacia la derecha tantas posiciones como indica el exponente.
Ejemplo:
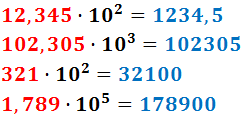Como los exponentes son positivos, la coma se desplaza hacia la derecha.
Si no hay suficientes cifras para desplazar la coma, se añaden 0's (a la derecha).
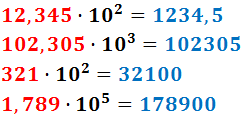
Si no hay suficientes cifras para desplazar la coma, se añaden 0's (a la derecha).
4. Multiplicar por una potencia de 10 con exponente Negativo
Anteriormente vimos que al dividir un número entre 10 la coma decimal de dicho número se desplaza una posición hacia la izquierda.
Como dividir sucesivamente (varias veces) entre 10 es lo mismo que multiplicar por una potencia de 10 con exponente negativo,
Al multiplicar un número por la potencia 10-n (con exponente negativo) se desplaza la coma hacia la izquierda tantas posiciones como indica el exponente (al cambiarle el signo).
Ejemplo:
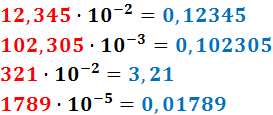
Como los exponentes son negativos, la coma se desplaza hacia la izquierda.
Si no hay suficientes cifras para desplazar la coma, se añaden 0's (a la izquierda). Esto ocurre en el primer, segundo y cuarto número del ejemplo.
Nota: el número resultante al cambiar el signo del exponente indica cuántas posiciones se desplaza la coma:
- 10-2: dos posiciones hacia la izquierda.
- 10-3: tres posiciones hacia la izquierda.
- 10-2: dos posiciones hacia la izquierda.
- 10-5: cinco posiciones hacia la izquierda.
Suma y resta en notación científica
Para sumar y restar números en notación científica, éstos deben tener el mismo exponente en la potencia de 10.
Una vez todos los números tienen el mismo exponente, tan sólo hay que sumar y restar los números que multiplican a la potencia de base 10, sacando factor común a la potencia de 10.
Para ello, hay que tener muy claro como modificar el exponente en un número en notación científica, ya que puede confundir bastante y llevar a error.
Por ejemplo, imaginemos que tenemos este número en notación científica:
y lo queremos expresar con 10 elevado a 5.
Al pasar de 10 elevado a 2 a 10 elevado a 5, la potencia de 10 está siendo 1000 veces mayor. Entonces, para mantener su valor, debemos hacer el número 1000 veces más pequeño, moviendo la coma 3 lugares hacia la izquierda:
Ahora lo queremos expresar con 10 elevado a -1. Al pasar de 10 elevado a 2 a 10 elevado a -1, estamos haciendo la potencia de 10 1000 veces más pequeña, por tanto, hay que hacer el número 1000 veces más grande, moviendo la coma 3 lugares hacia la derecha:
Vamos a ver otro ejemplo, pero esta vez con el 10 elevado a un número negativo:
Queremos expresarlo con 10 elevado a -2.
Al pasar de 10 elevado a -4 a 10 elevado a -2 estamos haciendo la potencia de 10 100 veces más grande (el exponente es menos negativo), por tanto debemos hacer el número 100 veces más pequeño moviendo la coma hacia la izquierda 2 lugares:
Ahora queremos expresarlo con 10 elevado a -6.
Al pasar de 10 elevado a -4 a 10 elevado a -6 estamos haciendo la potencia de 10 100 veces más pequeño (el exponente es más negativo), por tanto debemos hacer el número 100 veces más grande moviendo la coma hacia la derecha 2 lugares:
En general, si la potencia de 10 la hacemos más grande, el número hay que hacerlo más pequeño y viceversa.
Una vez tenemos esto claro, vamos a ver cómo sumar y restar en notación científica.
Por ejemplo, vamos a realizar la siguiente operación:
El segundo y el tercer término tienen un 3 en la potencia de 10. Sin embargo el primer término tiene un 2. Para poderlos sumar o restar, deben tener el mismo exponente en la potencia de 10.
Por tanto, hay que pasar el primer término de 10 elevado a 2 a 10 elevado a 3.
Al pasar de 10 elevado a 2 a 10 elevado a 3, la potencia de 10 se hace 10 veces mayor, por lo que el número hay que hacerlo 10 veces más pequeño, moviendo la coma un lugar hacia la izquierda:
Ahora ya tenemos todos los términos con exponente 3 en la potencia de 10:
Por tanto, vamos a proceder a sumar y restar los números:
Sacamos factor común a 10 elevado a 3 y operamos con los números:
Vamos a ver otro ejemplo con números negativos:
En esta caso, cada potencia de 10 tiene un exponente distinto. Debemos dejar todos con el mismo exponente. Por ejemplo voy a dejarlos todos con 10 elevado a -7 (podría ser cualquier exponente).
Vamos a pasar el primer término a 10 elevado a -7.
Al pasar de 10 elevado a -5 a 10 elevado a -7, la potencia de 10 se hace 100 veces más pequeña, por lo que el número hay que hacerlo 100 veces más grande, moviendo la coma dos lugares a la derecha:
Hacemos lo mismo con el segundo término. Al pasar de 10 elevado a -9 a 10 elevado a -7, la potencia de 10 se hace 100 veces más grande, por lo que el número hay que hacerlo 100 veces más pequeño, moviendo la coma dos lugares hacia la izquierda:
Ya tenemos todos los términos con potencias de 10 elevado a -7:
Tenemos que sumar y restar los números que tienen delante las potencia de 10:
Sacamos factor común a 10 elevado a -7 y operamos con los números:
Finalmente, dejamos el resultado en notación científica estándar, dejando el número que queda delante de al potencia de 10 entre 0 y 10, moviendo la coma hacia la izquierda y sumándole 1 al exponente:
Multiplicar y dividir en notación científica
Para realizar la multiplicación y división de números en notación científica, hay que tener en cuenta las propiedades de las potencias.
Cómo multiplicar números en notación científica
Para multiplicar números en notación científica, por un lado se multiplican los números que están delante de la potencia de 10 y por otro, se multiplican las potencias de 10, manteniendo la base y sumando los exponentes.
Por ejemplo:
Por un lado, multiplicamos los números y por otro las potencias de 10, manteniendo la base y sumando los exponentes:
Ahora movemos la coma un lugar hacia la izquierda y sumamos 1 al exponente para dejar el número en notación científica estándar:
Vamos a ver otro ejemplo donde uno de los números en notación científica tenga el exponente negativo:
Por un lado multiplicamos los números y por otro, al para multiplicar las potencias de 10, mantenemos la base y sumamos los exponentes, pero en este caso, sumamos un número negativo y al final es una resta. Debes tener claro que los exponentes se suman y la resta es consecuencia de sumar un número negativo:
Cómo dividir números en notación científica
La división con números en notación científica se realiza de forma similar a la multiplicación. Por un lado se dividen los números que están delante de la potencia de 10 y por otro, se dividen las potencias de 10, manteniendo la base y restando los exponentes.
Vamos a ver un ejemplo:
Por un lado, dividimos los números y por otro las potencias de 10, manteniendo la base y restando los exponentes:
Ten en cuenta, que cuando tengas un exponente negativo en la potencia de 10 del denominador, cuando restes los exponentes, al final se sumarán, por restar un número negativo, como por ejemplo:
Operaciones combinadas en notación científica
Vamos a ver ahora cómo realizar operaciones combinadas con números en notación científica, es decir, operaciones donde se mezclen sumas, restas, multiplicaciones y divisiones.
Tendremos que aplicar la jerarquía de operaciones y cada operación realizarla conforme acabamos de ver.
Por ejemplo:
En primer lugar, vamos a realizar al suma que está dentro del paréntesis. Para ello, los exponentes de las potencias de 10 deben ser iguales. Modificamos el número en notación científica del segundo término para que aparezca un -5 en el exponente:
Ahora realizamos la suma de dentro del paréntesis:
Seguimos realizando la multiplicación que queda en el numerador. Multiplicamos por un lado los números y por el otro las potencias de 10, manteniendo la base y sumando los exponentes:
Finalmente realizamos la división que queda. Dividimos los números por un lado y por el otro las potencias de 10, manteniendo la base y restando los exponentes:
Nos ha quedado 10 elevado a 0, que es 1. El resultado final lo pasamos a notación científica estándar:
Vamos a ver otro ejemplo:
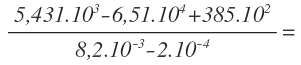
Vamos a empezar realizando las sumas y restas del numerador y del denominador. En el numerador transformamos los números para que aparezcan todos con potencias de 10 elevado a 3. En el denominador, lo hacemos para que las potencias de 10 estén elevadas a -3:
Ahora sumamos y restamos los números que quedan delante de la potencia de 10 tanto en el numerador como en el denominador:
Finalmente dividimos los números en notación científica:
